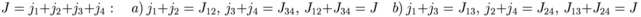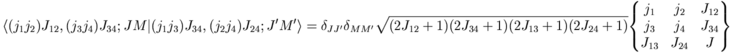List of Formulas
From FEFF
- The list of formulas used in FEFF
The corresponding soubroutines are quoted in the square bracket.
Parameter of angular momentum and quantum number kappa
The quantum number κ is a function of the orbital angular momentum quantum number l and the total angular momentum quantum number j.
κ = lΘ(l − j) − (l + 1)Θ(j − l)
where Θ(x) is equal to one if x is greater than zero and is equal to zero if x is less than zero. N.B. In the above equation the argument of Θ(x) can never equal zero since l is integral and j is half-integral.
The above equation is equivalent to:
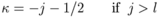
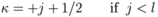
Density of States calculations
subroutine ff2rho
if (msapp != 1)
![\rho^c_{l}(E) = \rho^c_{l}(E)+\rm{Im}[\chi(E)]\rho^{sc}_l(E)\,](/feff/wiki/images/math/109ff6c43b9c5ccac0c36b82d3706363.png)
else
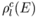
subroutine fmsdos
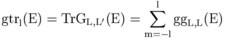
FMS calculations
XAS calculations
subroutine setkap(ihole, kinit, linit)
The contribution to the XAS from a given site  and orbital angular momentum
and orbital angular momentum 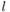 .
.
![\mu_{li}(E)=\mu{li}^{0\prime}(E)[1+\chi_{li}^\prime(E)]](/feff/wiki/images/math/6d68a89c6c341752fd939cdfd783cc4e.png) .
where
.
where  is the smoothly varying atomic background contributions and
is the smoothly varying atomic background contributions and 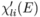 is the fine-structure or XAFS spectrum. A prime to denote final-state quantities calculated in the presence of a screened core hole.
is the fine-structure or XAFS spectrum. A prime to denote final-state quantities calculated in the presence of a screened core hole.
subroutine ff2xmu
Adds the contributions from each path and absorber, including Debye-Waller factors. Writes down main output: chi.dat and xmu.dat cchi(E) = S02 * TrG(E)
![\mu=\frac{\rm{rchtot}(E)}{\rm{xsedge}}=\rm{Im}[\rm{xsec}(E)+\rm{xsnorm}(E)*\chi_a(E)+\chi_i(E)]/\rm{xsedge}](/feff/wiki/images/math/19a456e4c73bacfd835759e0d2da8083.png)
Solving Dirac equations [afovrg]
The spin-orbit eigenfunction (eigenstates of 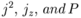 )
)
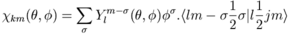
Matrix Elements for Electromagnetic Multipole Transitions (Grant) [xmult]
 , A = upexp(iω.r), | ω | = ΔE / c
where up is a polarization vector, and ω is the propagation vector.
, A = upexp(iω.r), | ω | = ΔE / c
where up is a polarization vector, and ω is the propagation vector.
Simplify the problem by taking ω to define the z-axis
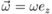 , so that we can write the polarization vector
, so that we can write the polarization vector
![u_p = \frac{1}{\sqrt{2}}\left[e_x+i p e_y\right]=-p\xi_p](/feff/wiki/images/math/25a636caeee17c4dcc07fdcea2135799.png) ,
, 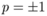 , where ξ0,ξ1,ξ − 1 are the usual spherical basis vectors.
, where ξ0,ξ1,ξ − 1 are the usual spherical basis vectors.
The decomposition of eik.r in terms of the irreducible tensors 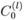
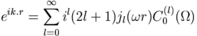 ,
where the angles involved are spherical polar coordinates with ez as polar axis.
,
where the angles involved are spherical polar coordinates with ez as polar axis.
The vector operator α is a tensor of order 1. The product of two tensors can be decomposed in terms of the irreducible tensors.
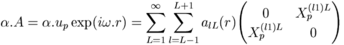 ,
where
,
where ![a_{lL}(r)=(-1)^L[L]^{1/2}\,i^l\begin{pmatrix}l&1&L\\0&-p&p\end{pmatrix}j_l(\omega r)](/feff/wiki/images/math/d273f4d0d6e0999cf5b12b68e41dfbe5.png)
In the form of Wigner-Eckart theorem:
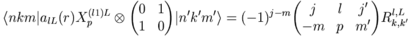
In the dipole approximation it is enough to keep only one term (l = 0, L = 1).
Note: the usual notation of atomic physics ![[k,l,\,...]=(2k+1)(2l+1)\,...](/feff/wiki/images/math/389966209ed7928db5e27d5d636677e5.png) .
.
subroutine xmult(k, kp, ls, lb, xm1, xm2)
- input:
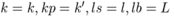
- output:
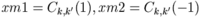
See Grant eq. 6.30. calculate the factors

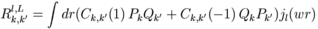
xm1, xm2 both either real or pure imaginary
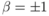 corresponds to the upper(lower) component of Dirac spinor.
corresponds to the upper(lower) component of Dirac spinor.
- calculate xm1 (β = 1 in eq.6.30)
- calculate xm2 (β = − 1 in eq.6.30)
![C_{k,k'}^{l,L}(\beta)=\sqrt{6}\left[j,L,j',\lambda,\lambda'\right]^{1/2}(-1)^{\lambda}\begin{Bmatrix}\lambda & l & \lambda' \\ \frac{1}{2} &\frac{1}{2} &1 \\ j & j' & L\end{Bmatrix}\begin{pmatrix}\lambda &l &\lambda' \\ 0 &0 & 0\end{pmatrix}\times\delta(\lambda,j-\frac{1}{2}\alpha\beta)\delta(\lambda',j'+\frac{1}{2}\alpha'\beta)](/feff/wiki/images/math/3963d5cd33f75315691c44f83790dad1.png)
Performs radial integration for multipole matrix element or central atom absorption [radint]
if ifl = 2
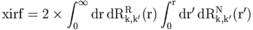
subroutine xrci ( mult, xm, dgc0, dpc0, p, q, bf, value)
- output: value
r-dependent multipole matrix element (before r-integration)
![dR_{k,k^\prime}^R(r)=P_k Q_{k^\prime}^R \left[C_{k,k^\prime}^{0,1}(-1)j_0(kr)+C_{k,k^\prime}^{2,1}(-1)j_2(kr)\right] +Q_k P_{k^\prime}^R\left[C_{k,k^\prime}^{0,1}(1)j_0(kr)+C_{k,k^\prime}^{2,1}(1)j_2(kr)\right]](/feff/wiki/images/math/4c64bc8efc1fb13664a415514571dea1.png)
dgc0*q* (xm(2)*bf(0) + xm(4)*bf(2)) + dpc0*p * (xm(1)*bf(0) + xm(3)*bf(2))
for double radial integral (use the irregular components of the final state)
![dR_{k,k^\prime}^N(r)=P_k Q_{k^\prime}^N \left[C_{k,k^\prime}^{0,1}(-1)j_0(kr)+C_{k,k^\prime}^{2,1}(-1)j_2(kr)\right] +Q_k P_{k^\prime}^N\left[C_{k,k^\prime}^{0,1}(1)j_0(kr)+C_{k,k^\prime}^{2,1}(1)j_2(kr)\right]](/feff/wiki/images/math/843ab198b7b6214788aefd3a09cd6d5e.png)
Radial Integration Routine
csomm (dr,dp,dq,dpas,da,m,np)
- output: da
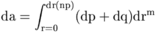 Modified to use complex p and q. SIZ 4/91
Modified to use complex p and q. SIZ 4/91
integration by the method of simpson of (dp+dq)*dr**m from 0 to r=dr(np)
dpas=exponential step; for r in the neighborhood of zero (dp+dq)=cte*r**da

Wigner 3j symbol [cwig3j]
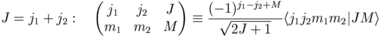
function cwig3j (j1,j2,j3,m1,m2,ient)
- input:
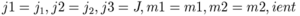
- output: wigner 3j coefficient for integers (ient=1) or semiintegers (ient=2) other arguments should be multiplied by ient
Orthogonality relations
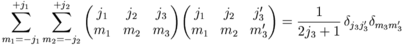
Composition relation for the spherical harmonics
![\int Y_{l_1}^{m_1}Y_{l_2}^{m_2}Y_{l_3}^{m_3} d\Omega = \left[\frac{(2l_1+1)(2l_2+1)(2l_3+1)}{4\pi}\right]^{\frac{1}{2}}\begin{pmatrix}l_1 & l_2 & l_3\\ 0 & 0 & 0\end{pmatrix}\begin{pmatrix}l_1 & l_2 & l_3\\ m_1 & m_2 & m_3\end{pmatrix}](/feff/wiki/images/math/0b1ace469ffac8f5a1c82690f1874d62.png)
6j symbols [sixj]
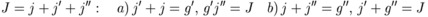
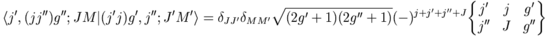
9j symbols [ninej]