POT: Scattering potentials

 

Initially the free atom potentials of each atomic type are calculated as if the atoms were isolated in space using a relativistic Dirac-Fock atom code. Scattering potentials are calculated by overlapping the free atom densities within the muffin tin approximation (Mattheiss prescription), and then including the Hedin-Lundqvist/Quinn self energy for excited states. Non overlapping muffin-tin radii are determined automatically from calculated the Norman radii. Automatic overlapping of muffin tin spheres (see the AFOLP card) is done by default, since it typically leads to better results than non overlapping muffin-tin spheres. FEFF8 can also calculate self-consistent potentials by successively calculating the electron density of states, electron density and Fermi level at each stage within a small cluster and then iterating, using the Mattheiss prescription for the initial iteration.

XAFS spectra are referenced to the threshold Fermi level. This quantity is best determined with the self-consistent field procedure (typically to within a fraction of an eV), or (less accurately but faster) can be estimated from the electron gas result at the mean interstitial density within Mattheiss prescription, as in FEFF7. An absolute energy scale is obtained by an atomic calculation of the total energy of the system with and without the core-hole. Atomic configurations and core-hole lifetimes are built in, and mean free paths are determined from the imaginary part of the average interstitial potential, including self-energy and lifetime contributions.

The potential calculations need as input only the atomic number of the atoms, and, for the absorbing atom, the type of the core hole being considered. To do the overlapping of the unique potentials, the neighboring atoms must be identified, either by position (from a list of the cartesian coordinates of each atom) or by explicit overlapping instructions using the OVERLAP card described in Section 2.3.

To save time the code calculates the overlapped atom potential for each unique potential only once, using as a sample geometry for an atom with a a given unique potential index that for the atom that is closest to the absorbing atom. Thus it is essential that the neighborhood of each sample atom be appropriate.

 AFOLP    folpx    (Standard)

This automatically overlaps all muffin-tins up to a specified maximum value (default folpx=1.15) to reduce the effects of potential discontinuities at the muffin-tins. Automatic overlapping is done by default and is useful in highly inhomogeneous materials. Typical values of the overlapping fraction should be between 1.0 and 1.3. See FOLP for a non-automated version. Automatic overlapping is done by default; to switch overlapping off, use 1.0 as the argument for AFOLP.

* touching muffin-tins; do not use automatic overlapping
AFOLP  1.0

 EDGE    label s02    (Standard)

The EDGE card is equivalent to the HOLE card, but you don't have to look up the appropriate integer index. Simply use the hole label: NO means no hole, K means K-shell, L1 means , and so on. As with the HOLE card you may also use the integer index instead of the label. All comments for HOLE card are valid for EDGE card - see the description below. Thus if the entry for is less than 0.1, will be estimated from atomic overlap integrals.

* L1-shell core hole, S02 = 1
  EDGE  L1   1.0

 HOLE    ihole s02    (Standard)

The HOLE card includes the hole-code index and the amplitude reduction factor . If the entry for is less than 0.1, then will be estimated from atomic overlap integrals. Experimental values of are typically between 0.8 and 1.0. The defaults if the HOLE card is omitted are ihole=1 for the K shell and =1. The hole codes are shown in Table 2.2.

FEFF is designed to calculate absorption from completely filled shells. You can try to simulate absorption from valence electrons with FEFF, but you may get unreliable results. If you encounter difficulties and need valence shell absorption, please contact the authors.

For , the core-hole lifetime parameter () is not tabulated in FEFF and is set equal to 0.1 eV, since the final state losses are then dominated by the self-energy. Use the EXCHANGE card to make adjustments ().

* K-shell core hole, S02 estimated by overlap integrals
  HOLE  1   0.0

  
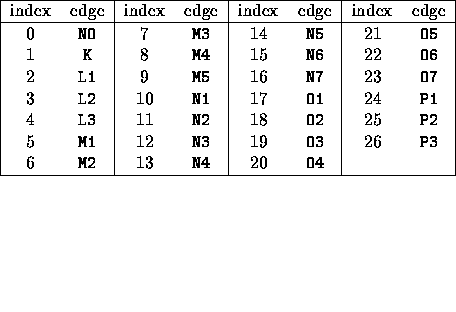
Table 2.2: Available hole codes. The entries in the columns marked edge are written as they are recognized by the EDGE card. Index 0, NO, is the no hole option described in the NOHOLE card.

 POTENTIALS        (Standard)

The POTENTIALS card is followed by a list which assigns a unique potential index to each distinguishable atom. The potential index ipot is the index of the potential to be used for the phase shift calculation. The list is of this form

  *    ipot   Z   [tag   lmax1   lmax2  xnatph]

The required list entries are the unique potential index ipot and the atomic number Z. The tag is at most 6 characters and is used to identify the unique potential in the 'path00.dat' output file. The optional list entries lmax1 and lmax2 are used to limit the angular momentum bases of the self-consistent potentials (XSPH) and full multiple scattering calculations (FMS). If a negative number (e.g., ) is specified for either lmax1 or lmax2, FEFF will automally use a default based upon the atomic number of the species normally lmax(atomic). The last optional entry xnatph can be used to specify the stoichiometric number of each unique potential in the unit cell of a crystalline material. This helps in the calculation of the Fermi level. In the case of an infinite solid, (default value) is a suitable value for the absorbing atom.

The absorbing atom must be given unique potential index 0. These unique potential indices are simply labels, so the order is not important, except that the absorbing atom is index 0, and you may not have missing indices (ie, if you use index 3, you must also have defined unique potentials 1 and 2).

To save time the code calculates the overlapped atom potential for each unique potential only once, using as a sample geometry the first atom in the atom list with a given unique potential index. Thus it is essential that the neighborhood of that sample atom be representative. Failure to do so may cause the code to generate inaccurate potentials and phase shifts and poor XAS results.

It is often useful to assume that the potential for a given shell of atoms is the same as that of a previously calculated shell in order to save calculation time. For example, in Cu it is a good approximation to determine potentials only for the central atom and the first shell and to use the first shell potential () for all higher shells. Such approximations should be checked in each case, however.

  * molecular SF6  Sulfur K edge, lamx1=default, lmax2=3 (spdf basis)
  POTENTIALS
  *   ipot     Z  tag  lmax1 lmax2
       0      16   S    -1    3  1
       1       9   F    -1    3  6

 S02    s02    (Standard)

The S02 card specifies the amplitude reduction factor . If the entry for is less than 0.1, then the value of is estimated from atomic overlap integrals. Experimental values of are typically between 0.8 and 1.0.

Alternatively, you can specify the value of in the HOLE or EDGE card; however, the meaning of the parameters in the 'feff.inp' file is more clear if you use the S02 card.

  * let FEFF calculate S02
  S02    0.0

 FOLP    ipot folp    (Useful)

The FOLP card sets a parameter which determines by what factor the muffin-tin radii are overlapped. We recommend that the AFOLP card be used in cases with severe anisotropy, and FOLP only be used for diagnostic purposes. Typically only values larger than 1 and less than 1.3 should be used. The AFOLP card will be ignored once FOLP is used for any potential type.

* -10% overlap of muffin tin with unique potential 0
*  10% overlap of muffin tin with unique potential 1
FOLP 0  0.9
FOLP 1  1.1

 EXCHANGE    ixc vr0 vi0 (ixc0)    (Useful)

The EXCHANGE card specifies the energy dependent exchange correlation potential to be used for the fine structure and for the atomic background. ixc is an index specifying the potential model to use for the fine structure and the optional ixc0 is the index of the model to use for the background function. The calculated potential can be corrected by adding a constant shift to the Fermi level given by vr0 and to a pure imaginary ``optical'' potential (i.e., uniform decay) given by vi0. Typical errors in FEFF's self-consistent Fermi level estimate are about 1 eV. (The CORRECTIONS card in Section 2.8 is similar but allows the user to make small changes in vi0 and vr0 after the rest of the calculation is completed, for example in a fitting process.) The Hedin-Lundqvist self-energy is used by default and appears to be the best choice for most applications we have tested in detail. The partially nonlocal model (ixc=5) gives slightly better results in some cases, but has not been tested extensively.

Another useful exchange model is the Dirac-Hara exchange correlation potential with a specified imaginary potential vi0. This may be useful to correct the typical error in non-self-consistent estimates of the Fermi level of about +3 eV and to add final state and instrumental broadening.

Defaults if EXCHANGE card is omitted are: ixc=0 (Hedin-Lundquist), vr0=0.0, vi0=0.0. For XANES, the ground state potential (ixc0=0) is used for the background function and for EXAFS the Hedin-Lundqvist (ixc0=0) is used.

Indices for the available exchange models:

0

Hedin-Lundqvist + a constant imaginary part

1

Dirac-Hara + a constant imaginary part

2

ground state + a constant imaginary part

3

Dirac-Hara + HL imag part + a constant imaginary part

5

Partially nonlocal: Dirac-Fock for core + HL for valence electrons + a constant imaginary part

*Hedin-Lundqvist -2eV edge shift and 1eV expt broadening
EXCHANGE 0 2. 1.

*Dirac-Hara exchange -3 eV edge shift and 5 eV optical potential
EXCHANGE 1 3. 5.

 NOHOLE        (Useful)

This card roughly simulates the effect of complete core-hole screening. It is useful to test the final state rule for calculated XAS, and to compare to other calculations (such as band structure or other codes) that do not use a core hole. The code will use as the final state that specified by the HOLE card for the matrix element calculation -- the NOHOLE card will cause FEFF to calculate potentials and phase shifts as if there is no core hole. For dDOS and or absorption calculations, for example, NOHOLE often gives better agreement for white line intensities. Conversely NOHOLE tends to give poor XANES intensities for K-shell absorption in insulators such as BN.

 RGRID    delta    (Useful)

The radial grid used for the potential and phase shift calculation is

with by default. The default is sufficient for most cases. However, occasionally there convergence problems in the atomic background at very high energies (the background curves upward) and in the phase shifts for very large atoms. If such convergence problems are encountered we suggest reducing delta to 0.03 or even 0.01. This will solve these problems at the cost of longer computation times (the time is proportional to ). This option is also useful for testing and improving convergence of atomic background calculations.

 SCF    rfms1 [lfms1 nscmt ca]    (Useful)

This card controls FEFF's automated self-consistent potential calculations. Thus all fields except rfms1 are optional. If this card is not specified then all calculations are done with the non self-consistent (overlapped atomic) potential. By default lfms1=0, nscmt=30 and ca=0.2.

rfms1

This specifies the radius of cluster for full multiple scattering during the self-consistency loop. Typically one needs about 30 atoms within sphere specified by rfms1. Usually this value is smaller than the value rfms used in the FMS card, but should be larger than the radius of the second coordination shell.

lfms1

The default value 0 is appropriate for solids; in this case the sphere defined by rfms1 is located on the atom for which the density of states is calculated. The value 1 is appropriate for molecular calculations and will probably save computation time, but may lead to inaccurate potentials for solids. When the center of the sphere is located on absorbing atom.

nscmt

This is the maximum number of iterations the potential will be recalculated. A value of 0 leads to non-self consistent potentials and Fermi energy estimates. A value of 1 also yields non-self consistent potentials but the Fermi energy is estimated more reliably from calculations of the LDOS. Otherwise, the value of nscmt sets an upper bound on the number of iterations in the self-consistency loop. Usually self-consistency is reached in about 10 iterations.

ca

The convergence accelerator factor. This is needed only for the first iteration, since FEFF uses the Broyden algorithm to reach self-consistency. A typical value is 0.2; however, you may want to try smaller values if there are problems with convergence. After a new density is calculated from new Fermi level, the density after the first iteration is . is extremely unstable and should not be used.

* Automated FMS SCF potentials for a molecule of radius 3.1 Angstroms
  SCF  3.1 1

 INTERSTITIAL    inters vtot    (Advanced)

The construction of interstitial potential and density may be changed by using INTERSTITIAL card. inters = ipot + 2*irav + 6*irmt. ipot=1 might be useful when only the surroundings of the absorbing atom are specified in 'feff.inp'. irav and irmt are described only for completeness and nonzero values are strongly not recommended.

ipot

defines how to find interstitial potential: ipot=0 (default) the interstitial potential is found by averaging over the entire extended cluster in 'feff.inp'. ipot = 1 the interstitial potential is found locally around absorbing atom.

irav

also changes how interstitial potential is found. 0 (default) equation for V_int is constructed at rav=r_nrm, 1 - at rav=(r_mt+r_nrm)/2 , 2 - at rav=r_mt

irmt

0 : Norman prescription for mt radii (default) 1 : Matching point prescription for mt radii (do not use)

vtot

is the volume per atom normalized by the volume ratmin**3 (), where ratmin is the shortest bond for the absorbing atom. This quantity defines total volume (needed to calculate interstitial density) of the extended cluster specified in 'feff.inp'. If vtot then the total volume is calculated as a sum of norman sphere volumes. Otherwise, ; where nat is a number of atoms in extended cluster. Thus vtot=1.0 is appropriate for cubic structures, such as NaCl. The INTERSTITIAL card may be useful for open systems (e.g. those which have ZnS structure.

* improve interstitial density for ZnS structures.
* vtot = (unit_cell_volume/number_of_atoms_in_unit_cell)/ratmin**3)=1.54
INTERSTITIAL  0 1.54

 ION    ipot ionization    (Advance)

The ION card ionizes all atoms with unique potential index ipot. Negative values and non-integers are permitted, however ionicities larger than 2 and less than -1 often yield unphysical results. Our experience with charge transfers using the SCF card suggests values for ionization about 5-10 times smaller than the formal oxidation state. The ION card is probably not needed if the potential is self-consistent. However, it can be used to put some total charge on a cluster. In this case we suggest using the same ionicity for all atoms in cluster (i.e. total ionization divided by number of atoms). For example, for diatomics like Br2, the fully relaxed configuration has a formal ionization of 1 on the scattering atom. Because of charge transfer, the actual degree of ionization is will be much smaller. In non-self-consistent calculations the default (non-ionized) scattering potentials are often superior to those empirically ionized, and the results should be checked both ways. The default if ION cards are omitted is that the atoms are not ionized.

* Simulates effective ionization for formal valence state +1
* ipot, ionization
  ION  1  0.2

 SPIN    ispin    (Advanced)

This card is used to specify the type of spin-dependent calculation. The complete description is given in Section G.1, when dealing with spin-dependent calculations.